Merge Sort in C#
Merge Sort is a popular sorting algorithm that is widely used in computer science and software development. It is an efficient, stable, and a divide-and-conquer algorithm that is based on the concept of merging two sorted arrays into one. The algorithm is particularly useful when working with large datasets, as it has a time complexity of O(n log n), which is considered to be one of the most efficient sorting algorithms. In this article, we will discuss how to implement Merge Sort in C# and its advantages and disadvantages.
The first step in implementing Merge Sort in C# is to create a method that will take in an array of integers as an argument. This method should then divide the array into two smaller arrays, sort them, and then merge them back together. The method should continue dividing the array until it reaches the base case, which is when the array is of size 1.
Custom Merge sort example
Here is an example of how to implement Merge Sort in C#:
class Sort
{
public static void MergeSort(int[] arr)
{
if (arr.Length <= 1)
return;
int mid = arr.Length / 2;
int[] left = new int[mid];
int[] right = new int[arr.Length - mid];
for (int i = 0; i < mid; i++)
left[i] = arr[i];
for (int i = mid; i < arr.Length; i++)
right[i - mid] = arr[i];
MergeSort(left);
MergeSort(right);
Merge(arr, left, right);
}
private static void Merge(int[] arr, int[] left, int[] right)
{
int i = 0, j = 0, k = 0;
while (i < left.Length && j < right.Length)
{
if (left[i] <= right[j])
arr[k++] = left[i++];
else
arr[k++] = right[j++];
}
while (i < left.Length)
arr[k++] = left[i++];
while (j < right.Length)
arr[k++] = right[j++];
}
static void Main()
{
int[] ints = { 8, 875, 7, 9, 764, 55 };
Console.WriteLine("Original array:");
foreach (int i in ints)
{
Console.WriteLine(i);
}
MergeSort(ints);
Console.WriteLine("Sorted array:");
foreach (int i in ints)
{
Console.WriteLine(i);
}
}
}
In the above code, the MergeSort() method is the main method that is responsible for dividing the array, sorting the sub-arrays, and merging them back together. The method checks if the array is of size 1 and returns if it is. If not, the method divides the array into two smaller arrays and calls the MergeSort() method recursively on each of them.
Once the sub-arrays are sorted, the method calls the Merge() method, which is responsible for merging the two sorted arrays back together. The Merge() method uses three pointers, i, j, and k, to iterate through the left and right arrays. The method compares the elements of the left and right arrays and assigns the smaller value to the original array. The method continues until all the elements in the left and right arrays have been added to the original array.
Visualization
You can imagine this sorting process as a tree of partition down to one element. That means every recursive call divides our array by 2. Take a look on the example below:
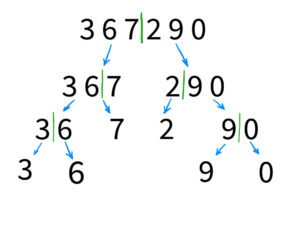
Here you can see how our array was divided. But the most interesting part is how it will be merged back:
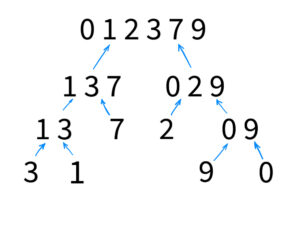
On this schema, you can see that the array sort itself during each merge. And this is the magic part of this sort. When you know that each part of the merged arrays is sorted, it is easier to put them together in sorted order.
You just have to go through them and check which value should go first and which after.
For example, let’s take the top of our recursive tree (1,3,7 and 0,2,9).
- We check the first values. 0 is the smallest so we push it as the first value to the result array ( Current state 1,3,7 and 2,9; Result array: 0 );
- We do the same with 1 and 2 ( Current state 3,7 and 2,9; Result array: 0,1 );
- We do the same with 2 and 3 ( Current state 3,7 and 9; Result array: 0,1,2 )
- We do the same with 3 and 9 ( Current state 7 and 9; Result array: 0,1,2,3 )
- We do the same with 7 and 9 ( Current state {} and 9; Result array: 0,1,2,3,7 )
- And finally just pushing 9 ( Current state {} and {}; Result array: 0,1,2,3,7,9 )
Pros and cons of the Merge sort
One of the advantages of Merge Sort is its stability. A sorting algorithm is said to be stable if two objects with equal keys appear in the same order in sorted output as they appear in the input array. This is important when sorting large datasets, as it ensures that the order of elements with the same key is preserved.
Another advantage of Merge Sort is its ability to handle large datasets. As the algorithm has a time complexity of O(n log n), it is able to efficiently sort large datasets without causing a significant performance hit. This makes it an ideal choice for applications that require sorting large amounts of data, such as databases, data analytics, and more.
One of the main disadvantages of Merge Sort is that it requires additional memory space to store the sub-arrays during the sorting process. This can be an issue when working with large datasets or systems with limited memory. Additionally, Merge Sort is not the best choice for small datasets, as the overhead of dividing and merging the arrays may not be worth the performance benefits.
Summary
In conclusion, Merge Sort is a powerful and efficient sorting algorithm that is widely used in computer science and software development. Its ability to handle large datasets and its stability makes it an ideal choice for many applications. However, it does require additional memory space, and may not be the best choice for small datasets. Understanding the advantages and disadvantages of Merge Sort will help you make an informed decision on whether or not to use it in your next project.
If you would know more about sorting algorithms in C#, follow the link.
Learn more with our Progress Academy!


