How to make a binary search in C#

Become a developer with our complete learning paths

Binary search in C#

Binary search is a powerful algorithm that allows you to quickly search for a specific value in a sorted array or list. This article will discuss how to implement a binary search in C# using the Array.BinarySearch() method, the IComparable interface, and the custom implementation of the binary search algorithm.

Prefer a VIDEO format? Check out our VIDEO TO THIS ARTICLE RIGHT HERE!

Oh, and if you feel overwhelmed with coding and getting hired as a coder, check out our developer membership (seriously, it’s worth it!). We help you become a job-ready developer and land your first programmer position.

Built-in Array.BinarySearch() method

To begin, let’s take a look at the Array.BinarySearch() method. This method is a built-in C# method that can be used to perform a binary search on an array. It takes two parameters: the array you want to search and the value you are looking for. It returns the index of the value if it is found, or a negative number if it is not found.

Here is an example of how to use the Array.BinarySearch() method:

int[] numbers = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };

int index = Array.BinarySearch(numbers, 5);

Console.WriteLine("The number 5 is at index " + index);

This example creates an array of integers and searches for the number 5. The output of this program will be “The number 5 is at index 4”, which is the index of the number 5 in the array.

Visual representation of the binary search algorithm

Binary search can be visualized as a process of repeatedly dividing a search interval in half.

The algorithm starts by comparing the middle element of the array or list with the target value.
If the target value is equal to the middle element, the search is complete and the index of the element is returned.
If it is less than the middle element, the search continues in the lower half of the array or list.
Otherwise, if the target value is greater than the middle element, the search continues in the upper half of the array or list.

Imagine we have a sorted array, and we want to find the index of 6 in it

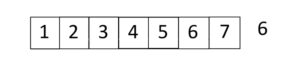
The first step will be to pick the middle value and check if it equals 6. If yes, we are done in one step.

Otherwise, we must check whether it is smaller or bigger than 6. If it is smaller, we will follow with the right side in the other case, we take a left.

In our example, 6 is bigger than 4. That means we will take the right part.

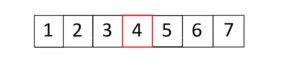
With this part, we have to repeat our manipulations. As you see, the middle value is 6. That means we are done with our search.

A custom binary search in C#

Another way to perform a binary search in C# is to use the IComparable interface. The IComparable interface is a built-in C# interface that allows you to define how to compare two objects of a certain type. By implementing this interface, you can create a custom binary or any other search algorithm that can be used with any type of object.

Here is an example of how to use the IComparable interface:

class Person : IComparable

{

public string Name { get; set; }

public int Age { get; set; }

public int CompareTo(object obj)

{

Person other = (Person)obj;

return this.Age - other.Age;

}

Here is the actual algorithm:

static int BinarySearch(Person[] people, Person person)

{

int left = 0;

int right = people.Length - 1;

while (left <= right)

{

int middle = (left + right) / 2;

int comparison = people[middle].CompareTo(person);

if (comparison == 0)

{

return middle;

}

else if (comparison < 0)

{

left = middle + 1;

}

else

{

right = middle - 1;

}

return -1;

}

Person[] people = { new Person { Name = "John", Age = 25 },

new Person { Name = "Jane", Age = 32 },

new Person { Name = "Bob", Age = 45 } };

int index = BinarySearch(people, new Person { Name = "", Age = 32 });

Console.WriteLine("Jane is at index " + index);

In this example, a custom class named “Person” is created with two properties, “Name” and “Age”. It implements the IComparable interface and defines the CompareTo method. The CompareTo method compares the ages of two Person objects. A binary search algorithm is then implemented that uses the CompareTo method to compare Person objects. The code then creates an array of Person objects and searches for a Person with an age of 32.

Check out our developer membership (seriously, it’s worth it!). We help you become a job-ready developer and land your first programmer position.

Learn more

Lost in coding? Discover our Learning Paths!